Electric cars are more massive, but not more dangerous to pedestrians
Or: A lot of people don't know what F = ma means
Contents
What to actually worry about in a collision
An intuition for why surface area matters and mass does not.
When you’re hit by a car, you want your legs to take all the force, NOT your head or chest
Technically, the thing that directly messes you up in a collision is actually pressure
Why does mass matter so much when two cars hit each other, and not when a car hits a pedestrian?
Background
I’m writing this in response to this thread. I don’t want people to think that EVs being more massive means they’re more dangerous for pedestrians, in part because I’m pro EV and want them to replace ICE cars, but also because I’d like people to understand everyday physics and what F = ma and p = mv actually mean. I studied physics in undergrad and taught high school physics for 7 years, and have a semi-popular physics YouTube channel here. If you have suggestions for this post please let me know at AndyMasley@gmail.com.
Does increasing the mass of a car make it more likely for pedestrians to be killed? No! Increasing front end height does though.
The only reason larger cars are more dangerous for pedestrians is their higher front ends, NOT the physical mass of the cars themselves. Even sedans are incredibly massive compared to people, and the difference in mass between a sedan and an electric hummer (a hummer’s about 2.8x as massive) is not enough to change the pedestrian’s experience on its own. More massive cars ARE much more dangerous for drivers inside smaller cars in car-on-car collisions, and if all cars had equal mass the roads would be much safer for drivers, but that’s a separate question from whether more massive cars are more dangerous for pedestrians. I explain the car-on-car collision situation at the bottom of the doc.
A funny intuition to prove this right away is to imagine that instead of the car moving toward you, you are moving toward the car and colliding with it. These situations are equivalent in classical mechanics. Let’s say that you run at a sedan at 10 mph and hit it, and then you run at an electric hummer (3x as massive) at 10 mph and hit it. The main reason you would be more hurt by the hummer is its larger front end area, not the fact that there’s so much more mass waiting for you. In both situations you probably would not meaningfully move the car at all with your force. They’re just two massive objects you can run into.
Incorrect reasons you may think the mass of the car matters
More massive cars are more difficult to slow down before hitting the pedestrian (shown by F = ma), so they will hit with higher speeds.
Why this is false: F = ma tells us that the larger the mass of a car, the more force is required to accelerate (in common language, decelerate) it by the same amount. However, this does NOT mean that it is more difficult for a DRIVER to slow down a car, because brake systems in larger cars account for the car’s larger mass and are designed to supply more force than brakes in smaller cars. Brakes are built to have the same effect on a car’s speed regardless of the car’s size so that drivers don’t have to supply 3x the force with their foot for cars that are 3x as large to have the same effect. Larger cars are not more difficult for drivers to slow down. This removes one candidate for the mass of the car mattering: speed of impact. Larger cars will hit pedestrians at the same speed as smaller cars will, because the driver’s reaction time and ability to affect the slowing will be the same in both.
More massive cars are more difficult for the pedestrian’s body to stop (shown by F = ma) so the collisions will be worse.
Why this is false: Pedestrians have basically no effect on a car’s speed, even for sedans at low speeds. If a sedan moving at 10 mph hits a stationary pedestrian, it will be slowed down to 9.5 mph and then keep going (shown in the table below). An electric hummer in comparison would slow from 10 mph to 9.8 mph. Not much of a difference! See the bullet point on p = mv below for how much difference in force the two collisions provide.
F = ma, so the more massive an object is, the more force it creates.
Why this is false: This is a misinterpretation of F = ma. F = ma describes how much force is required to accelerate a specific mass by a specific amount. It says nothing about how much force a mass “creates” or applies on another object. There IS a relationship between the mass of an object and the force it can supply in collisions, but this is much more complex and based on conservation of momentum and the relationship between change in momentum, time, and force. The relationship between a car’s momentum, mass, and force is explored in the next bullet point. If it were the case that F = ma solely determines how much force an object “creates” when it impacts another object, then an extremely large object moving toward you at 1 mile per hour (let’s imagine a mobile Mount Everest) would immediately kill you when it made physical contact with you instead of just gently pushing you forward.
p = mv. More massive cars supply more momentum to the pedestrian when they hit them, and because change in momentum equals force x time, they apply a larger force.
Why this is false: We can model a collision with a car and person as an inelastic collision (where two objects collide and stick together and move as one mass). Because of the conservation of momentum, the total momentum of the two objects before the collision equals the total momentum of the two objects moving together after the collision: mcar*vcar + mperson*vperson = (mcar + mperson)vafter-collision. The momentum supplied to the person by the car will equal the person’s mass times their final velocity (since their initial momentum is 0). I can make a table of the change in momentum and force on a person at different collision speeds for a midsize car and an electric hummer. A midsize car has a mass of about 1500 kg. An electric hummer has a mass of about 4100 kg. The average American has a mass of 86 kg. We can calculate the force on the person assuming a time of collision of 0.2 seconds and using the equation Δp = Ft, or F = Δp/t, where Δp is change in momentum.
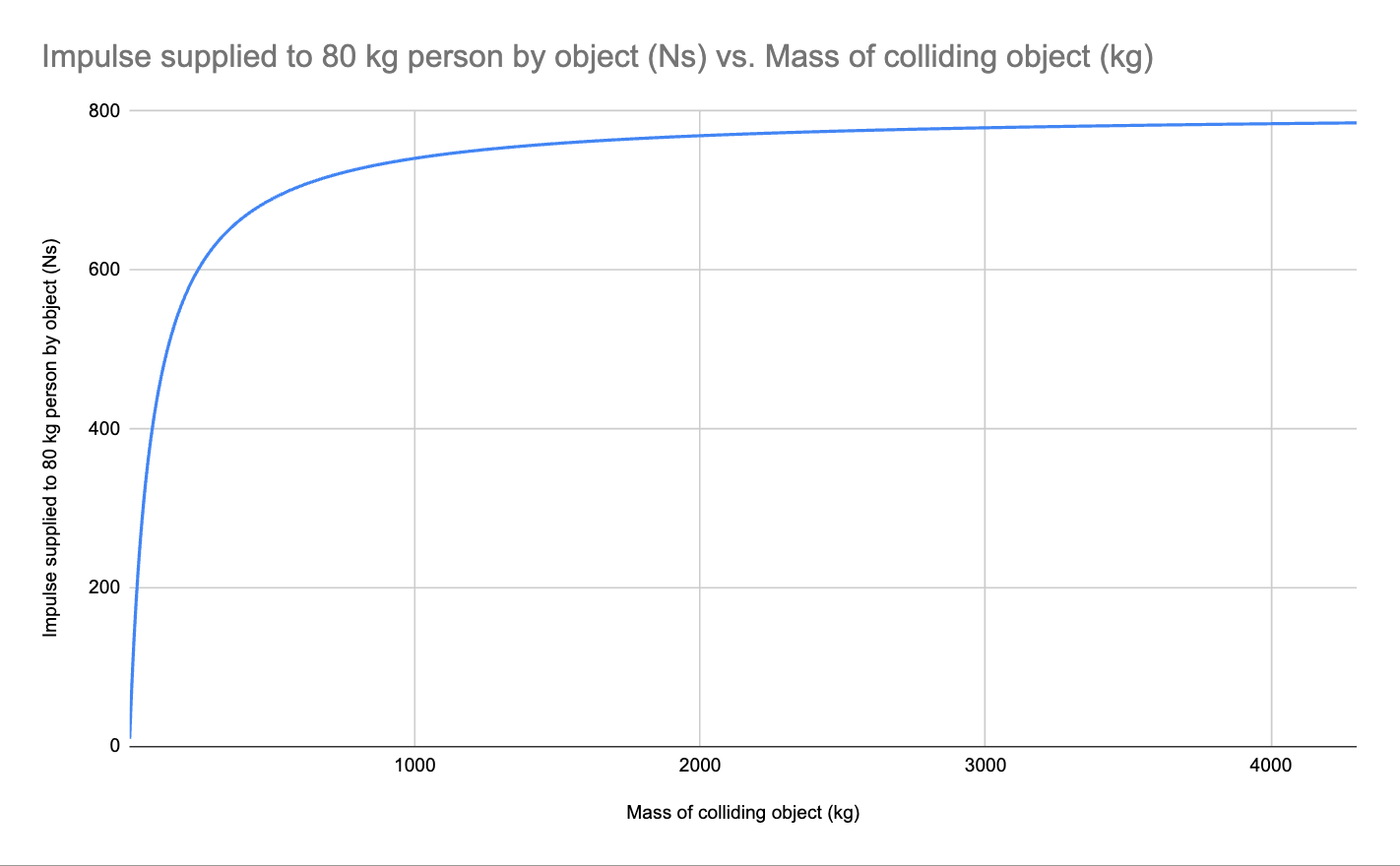
As you can see, the momentum and force supplied to the person in collisions with each car is basically the same, even though one car is 3x as massive as the other. If we were to increase the mass to infinity, the change in momentum of the person would approach an asymptote at the person’s mass times the car’s original speed, and no higher. Here’s a graph of the impulse supplied to a stationary 80 kg person in an inelastic collision at 10 m/s with an object at different masses:
Small cars like sedans have a mass of 1500 kg, which you can see is already very close to the asymptote of the graph. As you increase the mass beyond that, the impulse only slightly increases as it approaches the asymptote. This graph shows a reason why our intuitions fail us: in dealing with everyday objects (below 500 kg) the mass of the object matters a LOT in collisions. Getting hit with a bowling ball is very different than getting hit with a baseball. Our problem is we carry this forward and assume the almost vertical line on the graph increases forever, when in fact for very large objects it levels off and all collisions with an object above a certain mass are equally bad.
To intuit why this is the case, imagine seeing the Empire State Building moving toward you at 10 m/s. It hits you and begins to push you forward at 1 m/s along with it. Now imagine Mount Everest moving toward you at 10 m/s. It hits you and begins pushing you forward at 1 m/s. Do you think you would notice any difference between these two collisions in the force they supply on you? Probably not, even though Everest is MUCH more massive. Looking up at the graph, you can imagine that line staying flat as it approaches 800 Ns and the mass goes to infinity. The Empire State Building and Everest both lie far to the right on that flat line, and would each deliver about the same impulse (and therefore force) as the hummer and sedan. Cars (even sedans) are already so massive compared to humans that their difference in mass does not create much difference in the force they supply when they hit humans.
What to actually worry about in a collision
Surface Area!
Ultimately, the thing that puts pedestrians in danger is the size of the front of the car, because this determines whether their chest and/or head will be hit and receive force. This means that if we were to attach a vertical block of metal to the front of a sedan, it would become basically as dangerous for pedestrians as an EV hummer that’s 3x as massive.
What this implies is that bigger cars are in fact much more dangerous for pedestrians, but it’s entirely because of their volume (or more specifically the height of their front ends) rather than their mass.
An intuition for why surface area matters and mass does not
Which of these would you rather be hit by, assuming they move at the same speed?
Would your answer change if we stretched the limo to be even longer until it were 20,000 lbs, almost 5x the weight of the SUV? If not, this is a clue that what matters is the front end and not the mass of the vehicle.
When you’re hit by a car, you want your legs to take all the force, NOT your head or chest
Seems obvious. I’d much rather have a car hit my legs than my head at the same speed. With higher tops, cars impact your chest/head/other important body areas. That’s why larger cars kill more pedestrians.
Things that indirectly mess you up in a collision
Being pushed back onto the ground and hitting your head/other body parts on the ground.
Being pushed under the car and run over.
Not being pushed to the side of the car
The odds of these happening go way up when the front of the car is higher. With a low sedan, it’s more likely that you’ll fall onto the top of the car instead.
Technically, the thing that directly messes you up in a collision is actually pressure
This section is kind of a deviation from the main point but I want to clarify how the amount of force specifically affects the body
Pressure is equal to the force supplied on an area divided by the area itself. P = F/A. Each part of your body has a certain amount of pressure it can withstand before it breaks. The amount of time the pressure is applied for does not matter. If it’s above what that part of your body can handle, that part of your body will break/puncture. For example, it takes 100 lbs per square inch of pressure to puncture human skin, but you can puncture skin with much less than 100 lbs of force if you use a needle, because the needle has an extremely small surface area. Because P = F/A, making the A (area) extremely small makes the pressure extremely large, even if the force is a normal size. If you spread force applied over the length of a bone, the bone may not break, but if you concentrate the force on a very small surface area of the bone, the bone is more likely to break. This is not determined by how much time the force is applied for.
What determines whether a collision kills you is whether it supplies enough pressure on vital parts of your body, like your skull + brain or ribcage + heart.
A “collision” with a bullet is extremely bad, because even though a bullet has much less momentum (33.2 Ns, assuming a 0.04 kg bullet moving at 2700 mph) than a sedan moving at 1 mph (660 Ns), the force in the collision with the bullet is concentrated in an extremely small surface area (the tip), so it creates an extremely high pressure and will puncture your skin and break bones or destroy vital organs.
Differences in pressure don’t actually matter too much with large cars, because the force will always be equally spread out over the parts of your body that the car hits. What matters is not putting any significant force on the parts of your body that you depend on to survive (head + chest).
Why does mass matter so much when two cars hit each other, and not when a car hits a pedestrian?
Imagine that you’re hit with a grain of sand moving at 10 miles per hour, and then by 10 grains of sand clumped together all moving at 10 miles per hour. The clump is 10 times as massive as the grain, but neither will affect you much.
Now imagine that someone with half your weight runs at you at 10 miles per hour and hits you. Then, someone with twice your weight runs at you at 10 miles per hour and hits you. There would be a big difference between these two experiences!
Now imagine that the Empire State Building and Mount Everest can both slide across the ground. They are both moving at 10 miles per hour. When either one hits you, you’ll feel an immediate large force push you forward until you’re moving with them at 10 miles per hour like a fly stuck to a windshield, and their speed would not be meaningfully affected at all. Everest is MUCH more massive than the Empire State Building, but that difference in mass wouldn’t affect your experience.
What I’m trying to show with these examples is that when objects are much smaller or much larger than you, large differences in their mass don’t matter when you collide with them. However, when objects are around your size, differences in their mass make a big difference in how you experience collisions with them. Cars are the same. A pedestrian being hit by a car will not notice much difference if the car has a mass of 1000 kg or 4,000 kg. However if you’re in a 2000 kg vehicle, getting hit by a 1000 kg vehicle will be extremely different than getting hit by a 4000 kg vehicle. The reason why this works can be shown with math and the conservation of momentum.
Stopping distance does matter in a car-on-car collision, so F = ma does apply here
When two cars collide (let’s say here in a head-on collision), they apply the same force on each other (by Newton’s Third Law) and both begin to crumple as they slow the other. If one car requires a lot more force to stop, it will move forward much more before being stopped than the other car, damaging the other car. F = ma says that the more mass an object has, the more force is required to accelerate it by the same amount. Much more massive cars receive the same force as smaller cars in a collision, but their motion is affected much less by it, so they experience less change in momentum in the same time and therefore the driver of the larger car experiences much less of a force.
This is different than a car-pedestrian collision because a pedestrian has no hope of stopping the car with their body. The car is going to move right through them and carry them along with it.